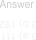Convolutional Layer

Convolution

Review the notes in Wintempla > Signal Processing > Convolution to learn more about convolution.
Lea las notas en Wintempla > Signal Processing > Convolution para aprender más sobre la convolución.

Problem 1
Solve the problem 1 in Wintempla > Signal Processing > Convolution .
Resuelva el problema 1 en Wintempla > Signal Processing > Convolution .

Problem 2
Create a Neural Lab project called ConvCalc to compute the convolution between two signals as shown; you only need a Main file.
Cree un projecto de Neural Lab llamado ConvCalc para calcular la convolución entre dos señales cómo se muestra; usted sólo necesitara un archivo Main.

ConvCalc\Main.lab
//_________________________________________ Main File
Vector x;
x.CreateSeries(1.0, 5.0, 5);
Vector y;
y.CreateSeries(10.0, 13.0, 4);
Vector result = Convolution(x, y);

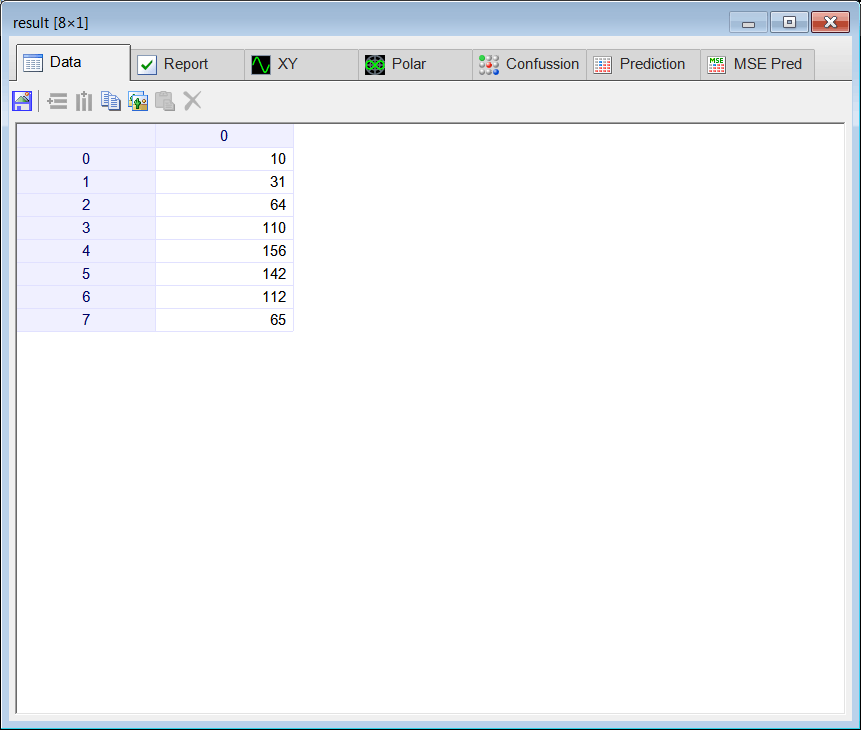
ConcCalcRun

Convolutional Filter

The figure below shows how to compute the output of a convolutional filter. In this case, the input has three rows and three columns. The filter has three rows, three columns and the bias. The output of the filter is computed by multiplying element by element the values in both matrices. Finally, all the values are added to compute the output value.
La figura de abajo muestra como se calcula la salida de un filtro convolucional. En este caso, la entrada tiene tres renglones y tres columnas. El filtro tiene tres renglones, tres columnas y la polarización. La salida del filtro se calcula multiplicando elemento por elemento los valores en ambas matrices. Finalmente, todos los valores se suman para calcular el valor de salida.

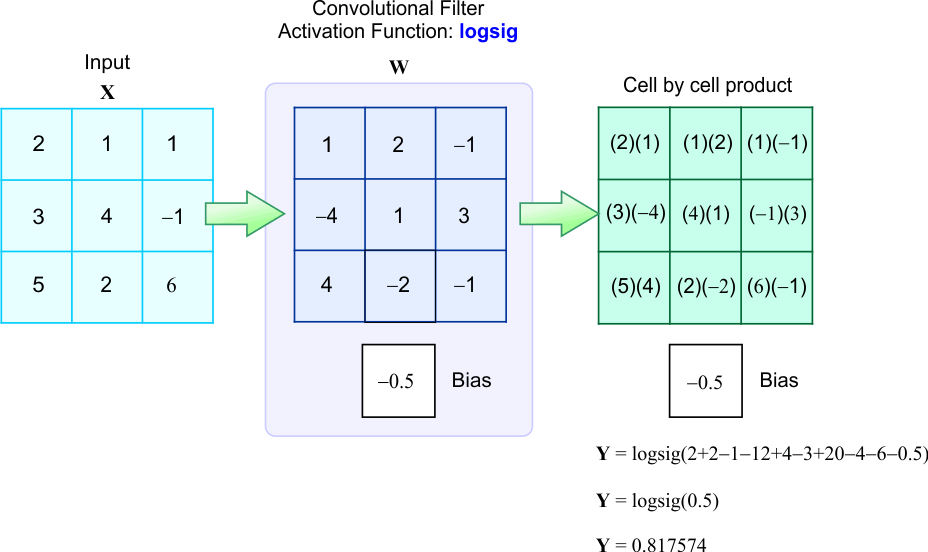
ConvFilter

2D Convolution

The figure below shows how 2D convolution is performed between matrix X and matrix W. First, we place matrix W on the corner at the top left of matrix X, then we multiply element by element the values in both matrices and the results of the multiplications are added together including the bias to produce one output value. Next, we shift matrix W one element to the right to compute another output value. The same process is repeated until all output values are computed.
La figura debajo muestra como la convolución en 2D se calcula entre la matriz X y la matriz W. Primero, se coloca la matriz W en la esquina superior izquierda de la matriz X, entonces se multiplican casilla por casilla los valores en las dos matrices y los resultados de las multiplicaciones se suman incluyendo la polarización. para producir un valor de salida. En seguida, se desplaza la matriz W una casilla a la derecha para calcular otro valor de salida. El mismo proceso se repite hasta que todos los valores se calculan.

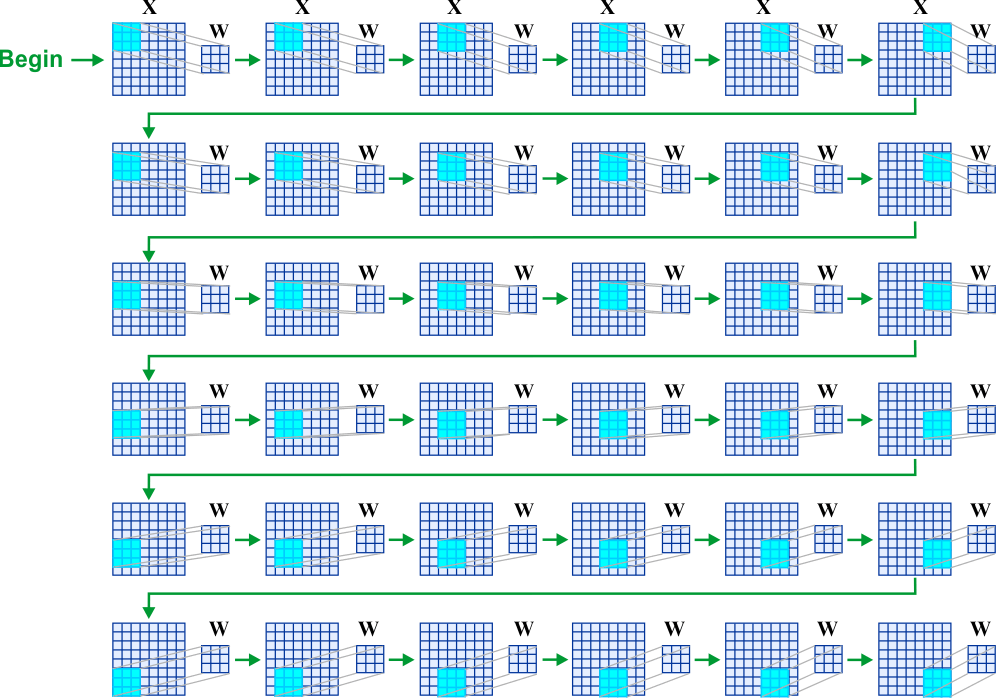
2DConvolution

Convolutional Layer

A convolutional layer is one type of layer commonly used in convolutional neural networks. The figure below shows a convolutional layer with one filter. The input of the layer, the X tensor has a width of 8, a height of 8 and a depth of 4. The convolution layer produces the output tensor Y with a width of 8, a height of 8 and depth of one. The filter has a set of weights including a weight for the bias. Because a convolutional layer can have one or more layers, a convolutional layer is a 4D tensor. In most cases, in a convolutional layer, the width and height of the output are equal to the width and the height of the input. That is, a convolutional layer does not change the width or the height of the tensor. However, a convolutional layer may change the depth of the tensor.
Una capa convolucional es un tipo de capa usada en las redes neuronales convolucionales. La figura de abajo muestra una red convolucional con un filtro. La entrada del filtro, el tensor X tiene un ancho de 8, una altura de 8 y una profundidad de 4. La capa convolucional produce el tensor de salida Y con ancho de 8, una altura de 8 y una profundidad de uno. El filtro tiene un conjunto de pesos incluyendo un peso para la polarización. En la mayoría de los casos, en una capa convolucional, el ancho y el alto de la salida son igual al ancho y a el alto de la entrada. En otras palabras, una capa convolucional no cambia el ancho o el alto del tensor. Sin embargo, una capa convolucional puede cambiar la profundidad del tensor.

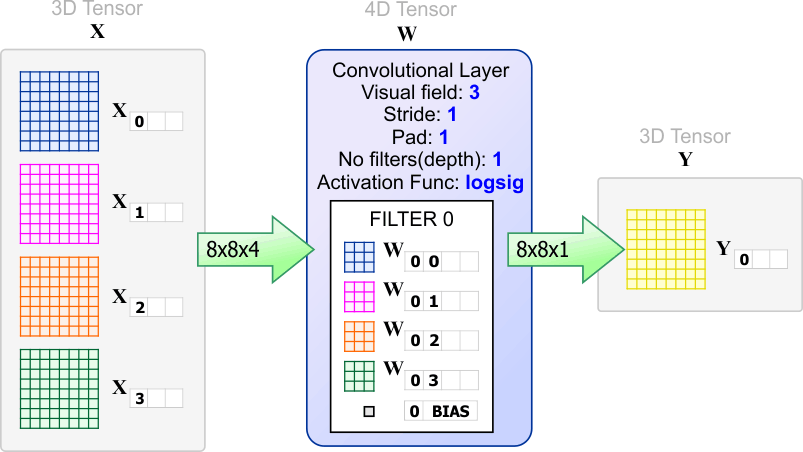
ConvLayer1

Tip
The figure below shows a convolutional layer with two filters. In this case, each filter produces a set of 64 values. Thus, the output tensor Y has a width of 8, a height of 8 and a depth of two. Observe that in this case, the convolutional layer does not change the width and the height of the tensor.
La figura de abajo muestra una capa convolucional con dos filtros. En este caso, cada filtro produce un conjunto de 64 valores. Por lo tanto, el tensor de salida Y tiene un ancho de 8, una altura de 8 y una profundidad de 2. Observe que en este caso, la capa convolucional no cambia el ancho ni la altura del tensor.

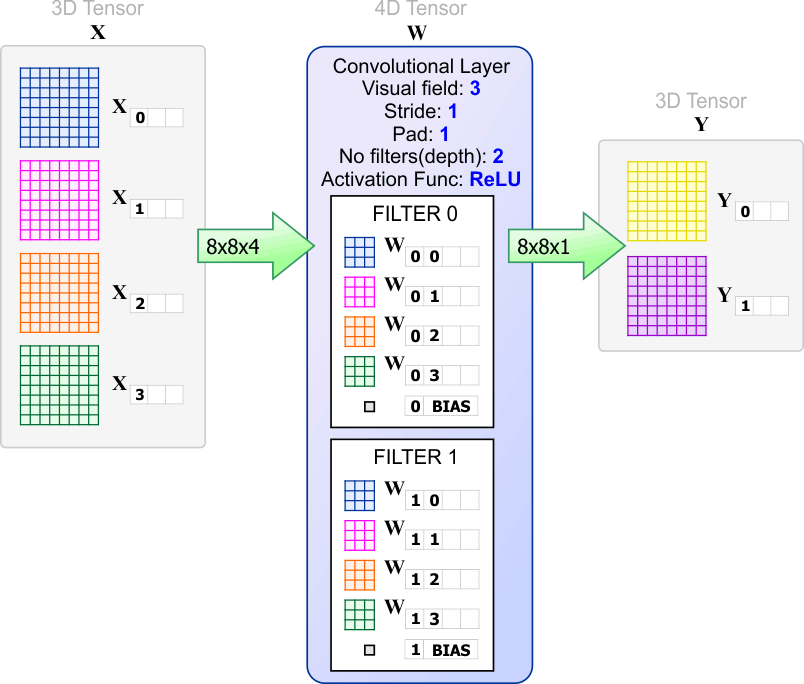
ConvLayer2

Tip
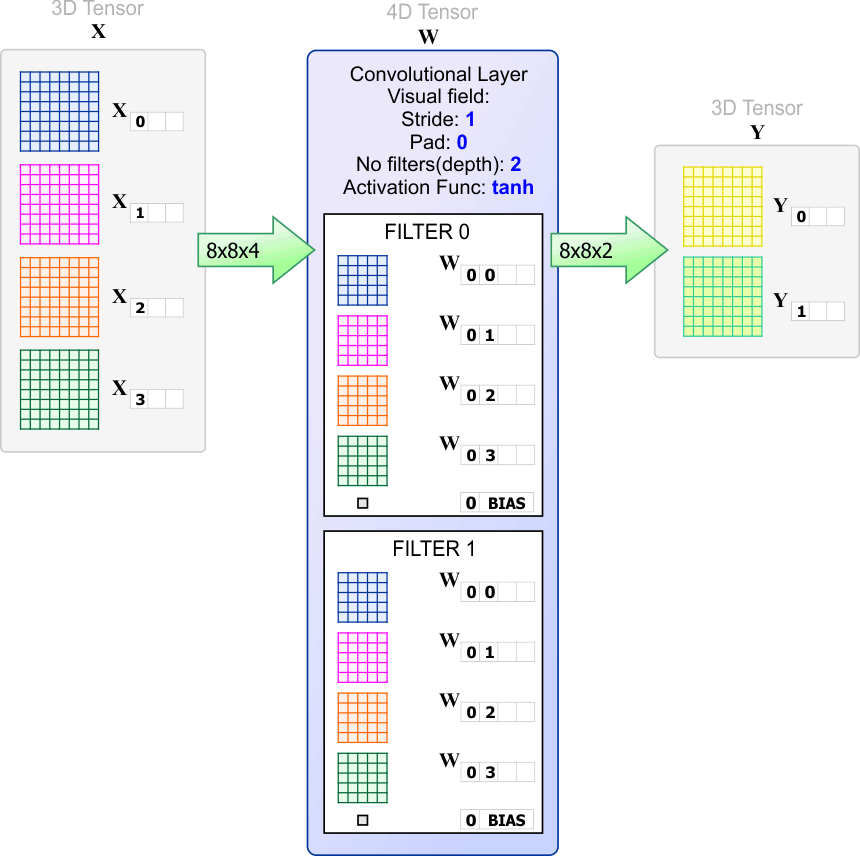
The filter shown below has a receptive field of three. In general, a filter is a set of weights (numbers). The values of these weights are dynamically computed during the training of the network. The convolutional layer in the figure has three filters. Observe that the depth of the input X must be equal to the depth of each filter. In this case, the depth of the input is four, therefore, each filter must have a depth of four. Observe that the depth of the output always is equal to the number of filters in the convolutional layer. The output tensor Y has a width of 8, a height of 8 and a depth of three. As before, the convolutional layer does not change la width nor the height of the tensor.
El filtro mostrado debajo tiene un campo receptivo de tres. En general, un filtro es un conjunto de pesos (números). Los valores de estos pesos son calculados dinámicamente durante el entrenamiento de la red. La capa convolucional en la figura tiene tres filtros. Observe que la profundidad de la entrada X debe ser igual a la profundidad de cada filtro. En este caso, la profundidad de la entrada es cuatro, por lo tanto, cada filtro debe tener una profundidad de cuatro. Observe que la profundidad de la salida siempre es igual al número de filtros en la capa convolucional. El tensor de salida Y tiene un ancho de 8, una altura de 8 y una profundidad de tres. Como antes, la capa convolucional no cambia el ancho ni el alto del tensor.

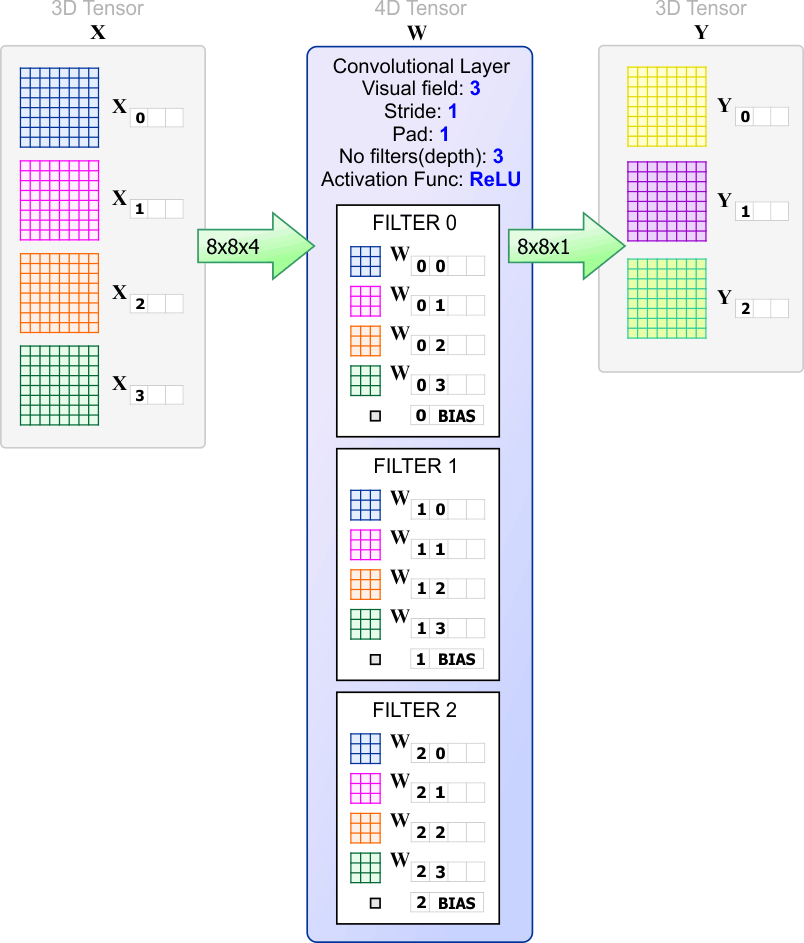
ConvLayer3

Problem 3
Compute the following from the convolutional layer shown in the previous figure:
  1. The total number of weights in the convolutional layer.
  2. The number of values in the output tensor Y.
Calcule lo siguiente de la red convolucional mostrada en la figura previa:
  1. El número total de pesos en la capa convolucional
  2. El número de valores en el tensor de salida Y.

Problem 4
Indicate what parameter o parameters must be equal between the input tensor and a convolutional layer.
Indique que parámetro o parámetros deben ser iguales entre el tensor de entrada y una capa convolucional.

Problem 5
Indicate what parameters must be equal between the output tensor and a convolutional layer.
Indique que parámetros deben ser iguales entre el tensor de salida y una capa convolucional.

Problem 6
  1. Indicate if the input tensor X is compatible with the convolutional layer shown.
  2. Indicate if the output tensor Y is compatible with the convolutional layer shown.
  3. Compute the number of weights in the convolutional layer.
  4. What is the value of the visual field of the convolutional layer?
  1. Indique si el tensor de entrada X es compatible con la capa convolucional mostrada.
  2. Indique si el tensor de salida Y es compatible con la capa convolucional mostrada.
  3. Calcule el número de pesos en la capa convolucional.
  4. Cual es el valor del campo visual de la capa convolucional?

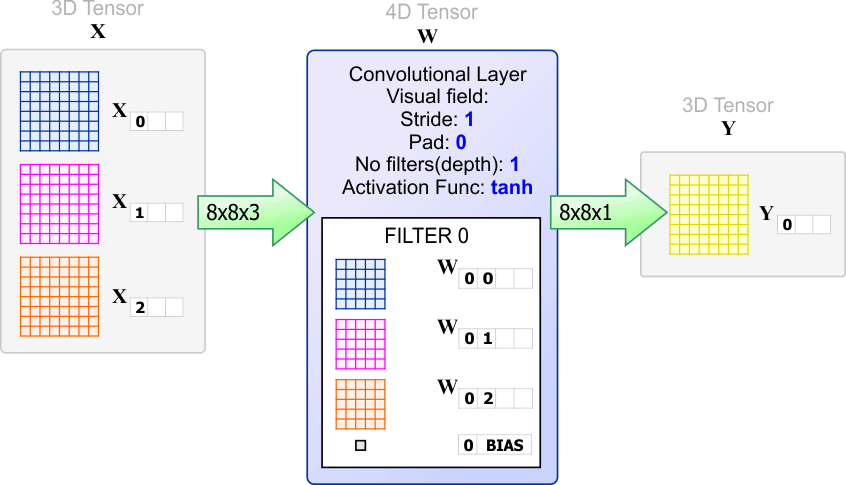
Filter5

Problem 7
  1. Indicate if the input tensor X is compatible with the convolutional layer shown.
  2. Indicate if the output tensor Y is compatible with the convolutional layer shown.
  3. Compute the number of weights in the convolutional layer.
  4. Compute the number of values in the output tensor Y.
  5. What is the value of the visual field of the convolutional layer?
  1. Indique si el tensor de entrada X es compatible con la capa convolucional mostrada.
  2. Indique si el tensor de salida Y es compatible con la capa convolucional mostrada.
  3. Calcule el número de pesos en la capa convolucional.
  4. Calcule el número de valores en el tensor de salid Y.
  5. Cual es el valor del campo visual de la capa convolucional?

Filter52

Problem 8
Create a program in your favorite programming language to compute the output of a convolutional layer. You will be able to test your program in the next problems.
  1. Program name: Convolution
  2. Code to send: Convolution.c, Convolution.cpp, Convolution.cs or Convolution.java
  3. Screenshot to send: Convolution.pdf
  4. Program Input:
    1. Input tensor (matrix array)
    2. Visual field (3, 5, 7, . . .
    3. Stride (0, 1, 2, . . .)
    4. Pad (0, 1, 2, . . .)
    5. Number of filters (1, 2, . . .)
    6. Activation function: logsig, tanh, ReLU or Linear
  5. Program Output: Output tensor (matrix array)
Cree un programa en su lenguaje favorito de programación para calcular la salida de una capa convolucional. Usted tendrá la oportunidad de probar su programa en los próximos problemas.
  1. Nombre del programa: Convolution
  2. Código para enviar: Convolution.c, Convolution.cpp, Convolution.cs o Convolution.java
  3. Captura de pantalla para enviar: Convolution.pdf
  4. Entrada del programa:
    1. Tensor de entrada (un arreglo de matrices)
    2. Campo visual (3, 5, 7, . . .
    3. Saltos (0, 1, 2, . . .)
    4. Relleno (0, 1, 2, . . .)
    5. Número of filtros (1, 2, . . .)
    6. Función de activación: logsig, tanh, ReLU o Lineal
  5. Salida del programa: Tensor de salida (un arreglo de matrices)

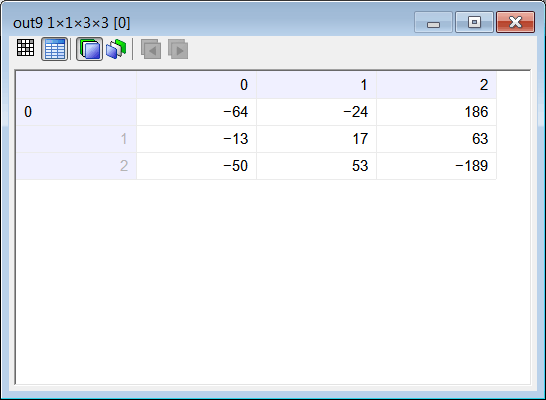
Problem 9
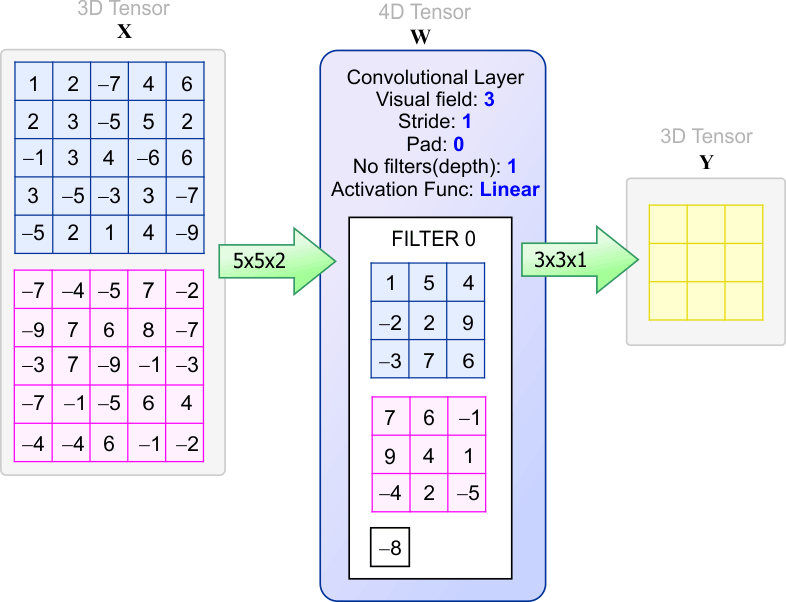
Compute the values in the output tensor Y using your program.
Calcule los valores en el tensor de salida Y usando su programa.

ConvProblem

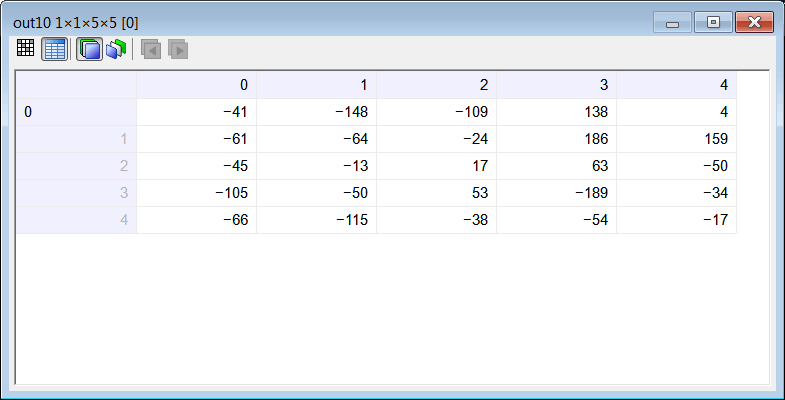
Problem 10
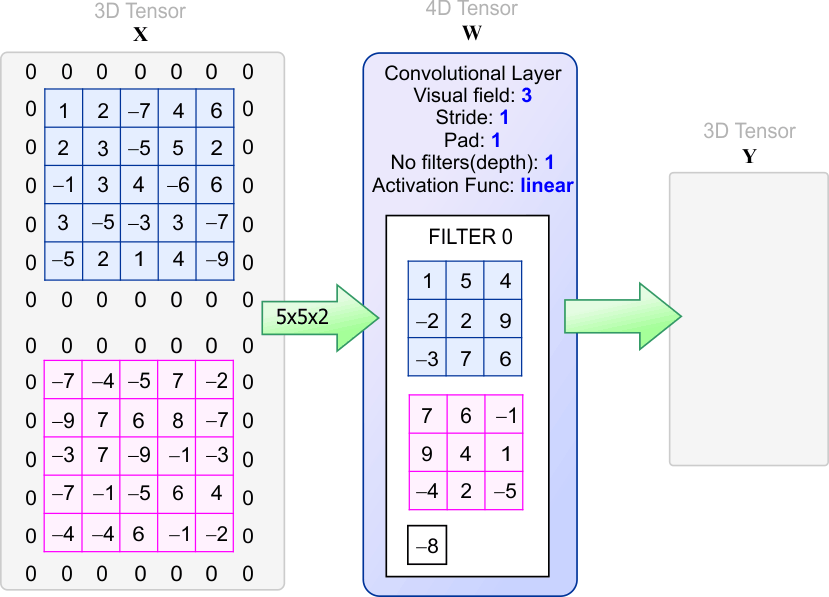
Compute the values in the output tensor Y using your program.
Calcule los valores en el tensor de salida Y usando su programa.

PadProblem

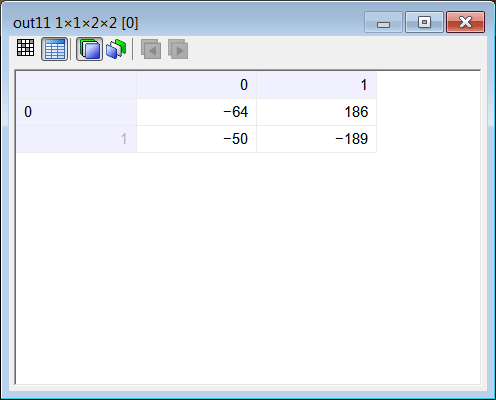
Problem 11
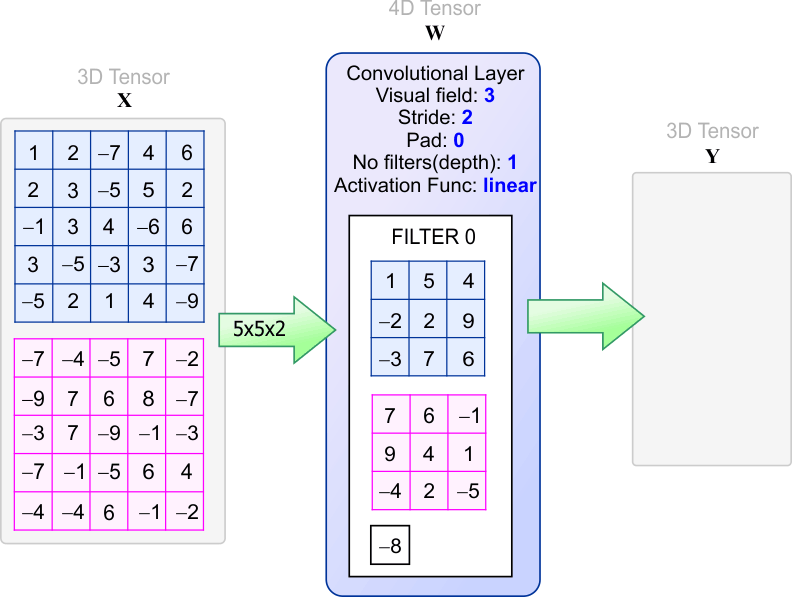
Compute the values in the output tensor Y using your program.
Calcule los valores en el tensor de salida Y usando su programa.

StrideProblem

Problem 12
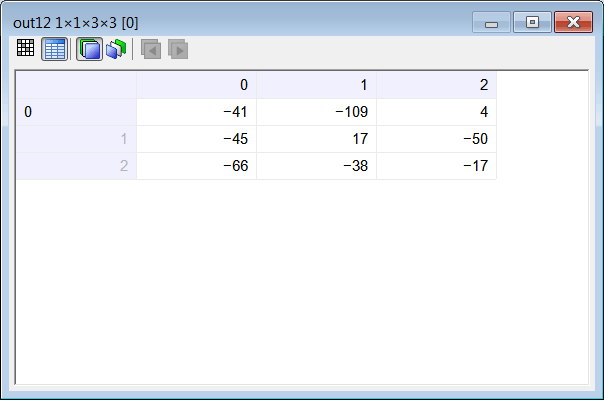
Compute the values in the output tensor Y using your program.
Calcule los valores en el tensor de salida Y usando su programa.

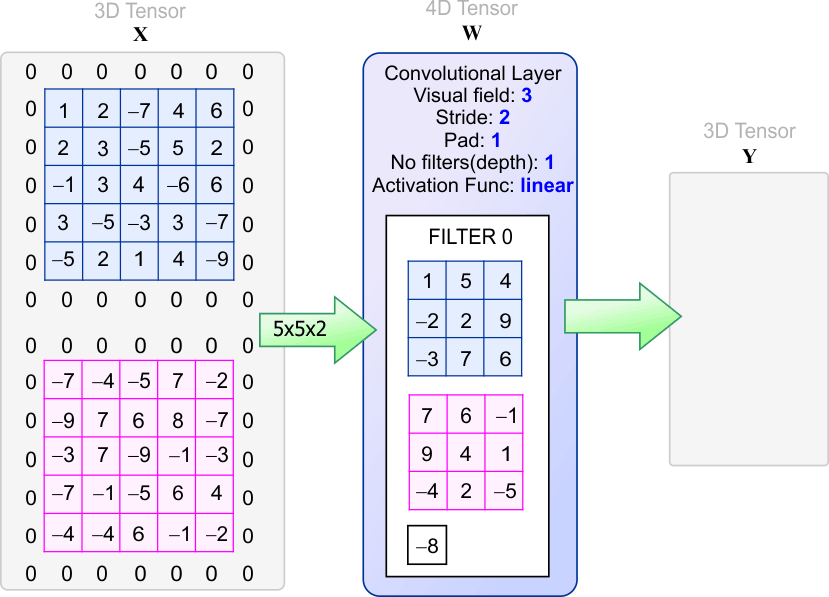
PadStrideProblem

Problem 13
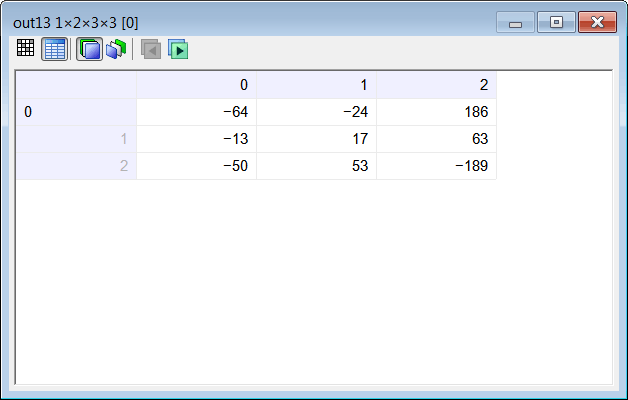
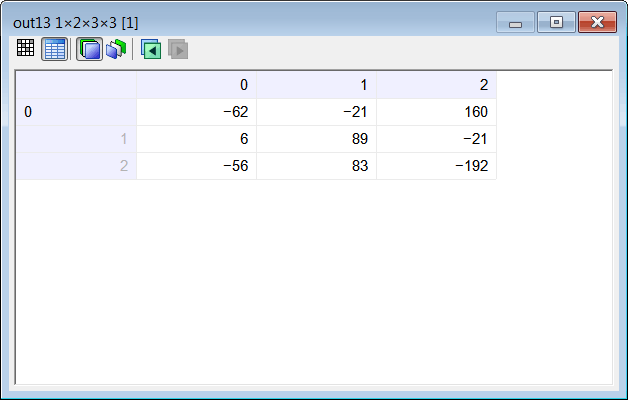
Compute the values in the output tensor Y using your program.
Calcule los valores en el tensor de salida Y usando su programa.

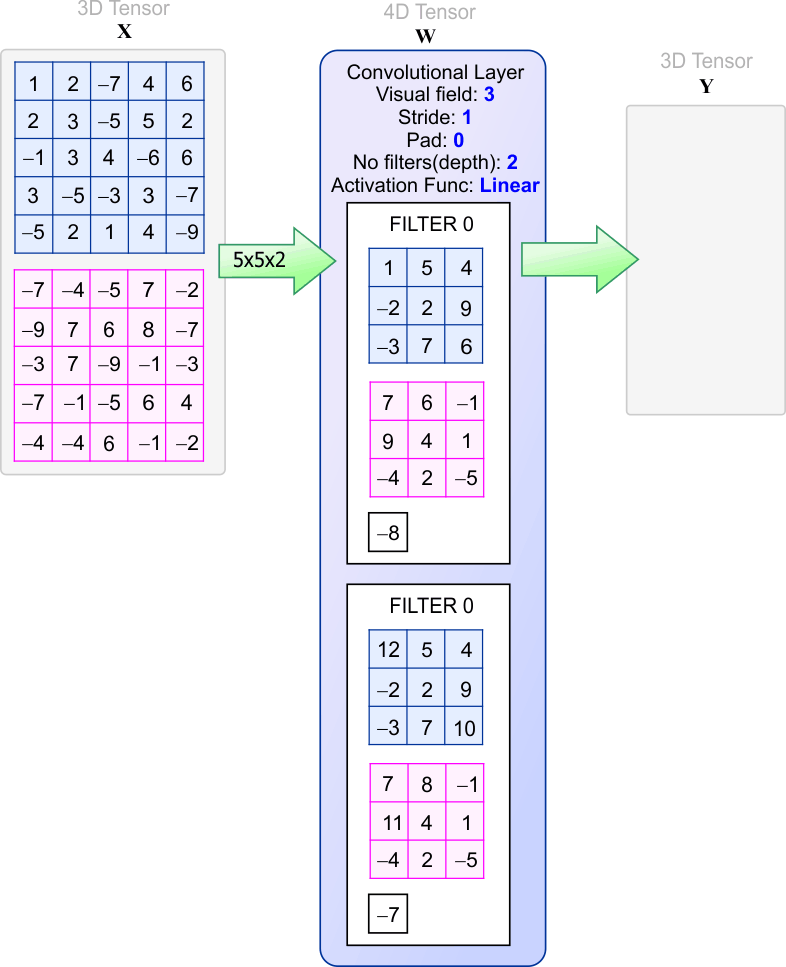
ConvTwoFilters

Problem 14
Create a Neural Lab project Cruconv with a Main file to verify the answers of the previous problems. You can re-use the input.csv file that you created in Convolutional NN > Pooling .
Cree un proyecto de Neural Lab llamado Cruconv con un archivo Main para verificar las respuestas de los problemas anteriores. Usted puede re-usar el archivo input.csv que fue creado en Convolutional NN > Pooling .

Step A
Use notepad or Microsoft Excel to create the file filterA.csv and filterB.csv. Store the files inside the Cruconv folder, be sure you to save the files as .csv but not as .csv.txt.
Use el block de notas o Microsoft Excel para crear los archivos filterA.csv y filterB.csv. Guarde el archivo dentro de la carpeta Cruconv, asegúrese de guardar los archivos como *.csv y no como *.csv.txt.

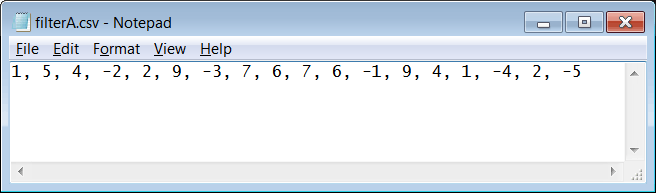
filterAcsv

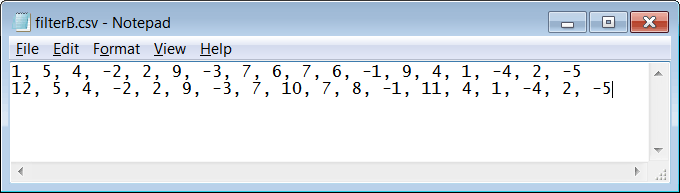
filterBcsv

CruconvFolder

Step B
Edit the Cruconv.lab file. Run the program and double click each of the output tensors to review the data.
Edite el archivo Cruconv.lab. Ejecute el programa y haga clic doble en cada uno de los tensores de salida para revisar los datos.

Cruconv\Main.lab
//____________________________________ 1. Load Input
Tensor input;
int depth = 2;
int height = 5;
int width = 5;
input.LoadCsv(depth, height, width);
//____________________________________ 2. Create network
int visualField = 3;
int stride = 1;
int pad = 0;
ConvNet net;
net.Create(5, 5, 2, 1);
net.SetInRange(1.0, 1.0); // No input scaling
net.SetOutRange(1.0, 1.0); // No output scaling
//____________________________________ 3. PROBLEM 9
net.SetConvLayer(0, 0, visualField, pad, stride, 1); //Activation function: linear=0
Tensor filterA;
filterA.LoadCsv(3, 3, 2);
Vector bias;
bias.Create(1);
bias[0] = -8;
net.SetWeights(0, filterA, bias);
Tensor out9;
net.Run(input, out9);
//____________________________________ 4. PROBLEM 10
pad = 1;
net.SetConvLayer(0, 0, visualField, pad, stride, 1); //Activation function: linear=0
net.SetWeights(0, filterA, bias);
Tensor out10;
net.Run(input, out10);
//____________________________________ 5. PROBLEM 11
stride = 2;
pad = 0;
net.SetConvLayer(0, 0, visualField, pad, stride, 1); //Activation function: linear=0
net.SetWeights(0, filterA, bias);
Tensor out11;
net.Run(input, out11);
//____________________________________ 6. PROBLEM 12
stride = 2;
pad = 1;
net.SetConvLayer(0, 0, visualField, pad, stride, 1); //Activation function: linear=0
net.SetWeights(0, filterA, bias);
Tensor out12;
net.Run(input, out12);
//____________________________________ 7. PROBLEM 13
Tensor filterB;
filterB.LoadCsv(2, 3, 3);
bias.Create(2);
bias[0] = -8;
bias[1] = -7;
stride = 1;
pad = 0;
net.SetConvLayer(0, 0, visualField, pad, stride, 2); //Activation function: linear=0
net.SetWeights(0, filterB, bias);
Tensor out13;
net.Run(input, out13);





out9

out10

out11

out12

out130

out131

Problem 15
Do you recommend to use a fully connected layer before a convolutional layer? Explain your answer.
Recomienda usted usar una capa completamente conectada antes de una capa convolucional? Explique su respuesta.

Problem 16
Open the Grocery project that you created in Convolutional NN > Tensor . Add a new file called FruitConv.lab to test a convolutional layer with two filters, one to detect horizontal borders and another one to detect vertical borders. After creating the project use notepad to create a CSV file called filter.csv. Observe that each filter has 27 elements: 9 elements are for the red component, 9 elements are for the green component and 9 elements are for the blue component.
Abra el proyecto de Grocery que usted creo en Convolutional NN > Tensor . Agregue un archivo nuevo llamado FruitConv.lab para probar una capa convolucional para detectar bordes horizontales. Después de crear el proyecto use el block de notas para crear un archivo CSV llamado filter.csv. Observe que cada filtro tiene 27 elementos: 9 elementos para el componente rojo, 9 elementos para el componente verde y 9 elementos para el componente azul.

filterCsv

Grocery\FruitConv.lab
//______________________________ 1. Load the tensor
Tensor fruit;
fruit.LoadFolder();
//______________________________ 2. Create the network
int visualField = 3;
int stride = 1;
int actiFunc = 0; //Linear
int pad = 0;
ConvNet net;
net.Create(256, 256, 3, 1);
net.SetInRange(0.0, 255.0);
net.SetConvLayer(0, actiFunc, visualField, pad, stride, 2);
Tensor filter;
filter.LoadCsv(3, 3, 3);
Vector bias;
bias.Create(2);
bias[0] = 0.0;
bias[1] = 0.0;
net.SetWeights(0, filter, bias);
//______________________________ 3. Run
Tensor output;
net.Run(fruit, output);

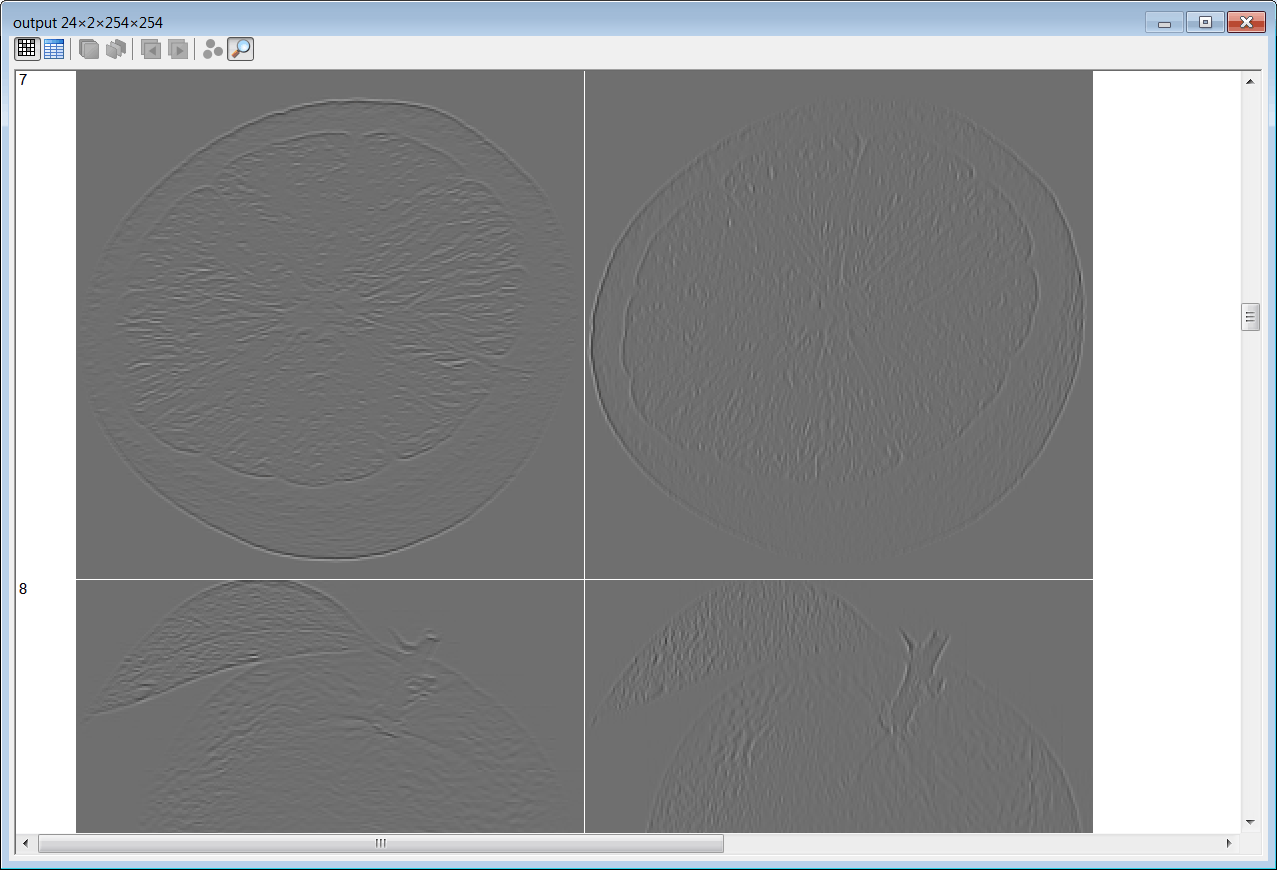
fruitFilterRun

Tip
In a convolutional neural network, the filters are dynamically adjusted during training.
En una red neuronal convolucional, los filtros son dinámicamente ajustados durante el entrenamiento.

answer

© Copyright 2000-2021 Wintempla selo. All Rights Reserved. Jul 22 2021. Home